Convex Curves: A Reminder on Price Convexity and Cap-Rate Volatility

In other words, the relationship between the dollar value of price changes is non-linear (and convex) with regard to the basis-point change in cap rates.² For purposes of illustration, let’s assume certain real estate investors (and lenders) are either: estimating today’s market-clearing cap rate to equal 5%, or forecasting an ending (or reversionary) cap rate of 5%.³ In either case (depending on the investor’s objectives), let’s assume net operating income (NOI) of $500 so that the property’s price (today or in the future) equals $10,000:⁴

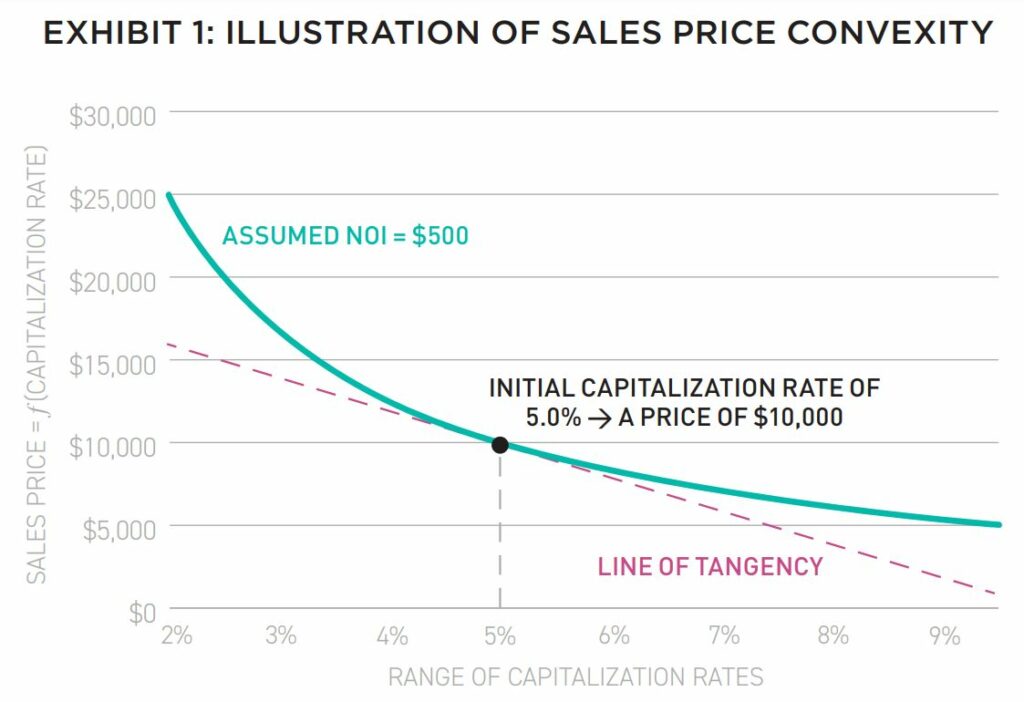
Let’s revisit this simple illustration of price convexity by considering a 100 basis-point change in the cap rate, from the assumed starting point of a 5% initial cap rate, as shown in Exhibit 2.

As indicated in Exhibit 2, decreasing the initial cap rate by 100 basis points results in an ending cap rate of 4% and an increase in the sales price to $12,500, for an increase of 25% from initial estimate of $10,000.

Meanwhile, increasing the initial cap rate by 100 basis points results in an ending cap rate of 6% and a decrease in the sales price to approximately $8,333, for a decrease of approximately 16.7%.

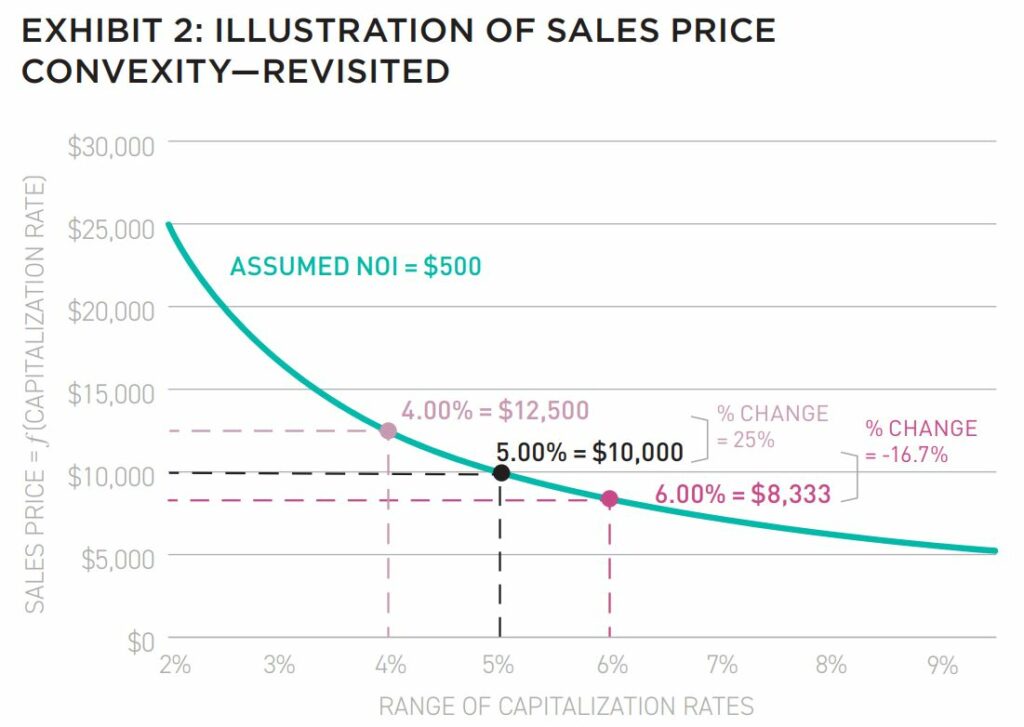
This difference (i.e., 25% v. -16.7%) illustrates the convexity in real estate prices for a given change in cap rates. Said another way, convexity implies that the percentage change in price varies with a constant change (measured in basis points) in cap rates.

Given today’s conversations about the potential increases in interest rates and cap rates, the convexity in real estate prices suggests that the fall (measured by the percentage change) in prices due to rising cap rates is less than the earlier benefits associated with heretofore falling cap rates. This is, of course, “cold comfort” to investors (and lenders).

SKEWED V. SYMMETRICAL VOLATILITY ESTIMATES

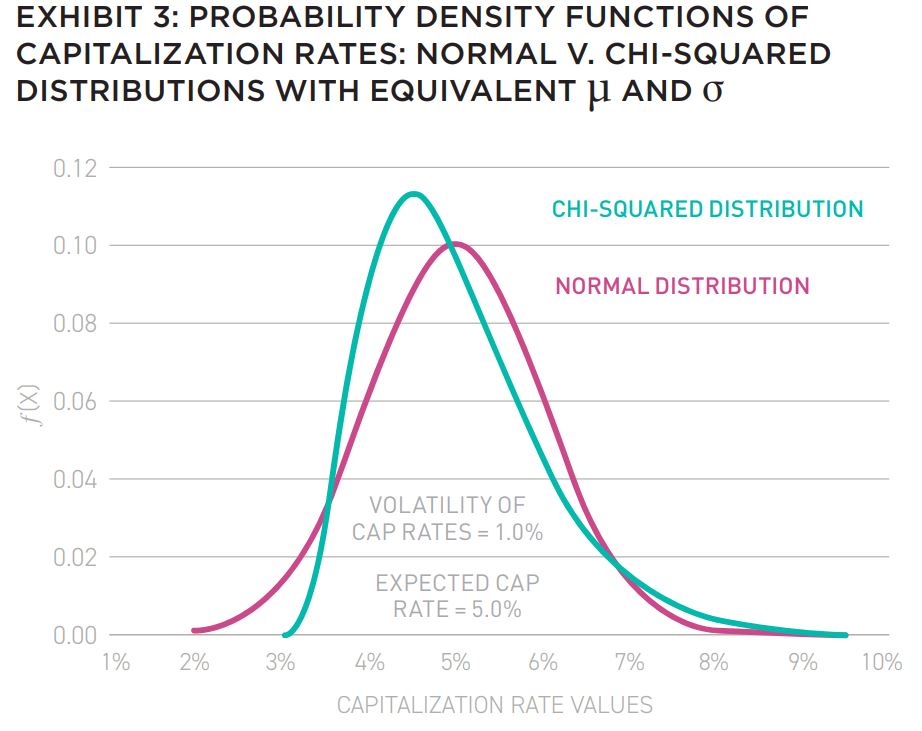
The importance of convexity is also highlighted when we consider the distribution of potential (current and/or reversionary) cap rates. As suggested earlier, such distributions may not be normally distributed. So as an illustration, let’s compare the hypothetical in which the distribution of cap rates is modeled by the symmetrical normal distribution and by the asymmetrical chi-squared (or χ2 ) distribution, where both distributions5 have the same expected value and the same volatility: µ = 5% and σ = 1% (these values were arbitrarily chosen – investors should select parameters consistent with their expectations), as shown in Exhibit 3:

Other asymmetrical distributions are, of course, possible and would also serve to help make the points below.6 While both distributions have (by design) the same first two moments (µ = 5% and σ = 1%), the chi-squared distribution displays positive skewness: fewer instances of extremely low cap rates and a mode of ≈4.5% (as compared to a mean of 5%). On the other hand, the normal distribution displays the familiar bell-shaped (symmetrical) distribution, but importantly includes greater instances of extremely low cap rates. It is these extremely low cap rates that produce correspondingly extremely high property prices. The two distributions’ far-right tails (i.e., high cap rates) ae similar, and therefore produce similar estimates of extremely low property prices.

Against this backdrop of price convexity and capitalization-rate dispersion, let’s consider the potential dispersion in (current and/ or reversionary) property values, as shown in Exhibit 4:

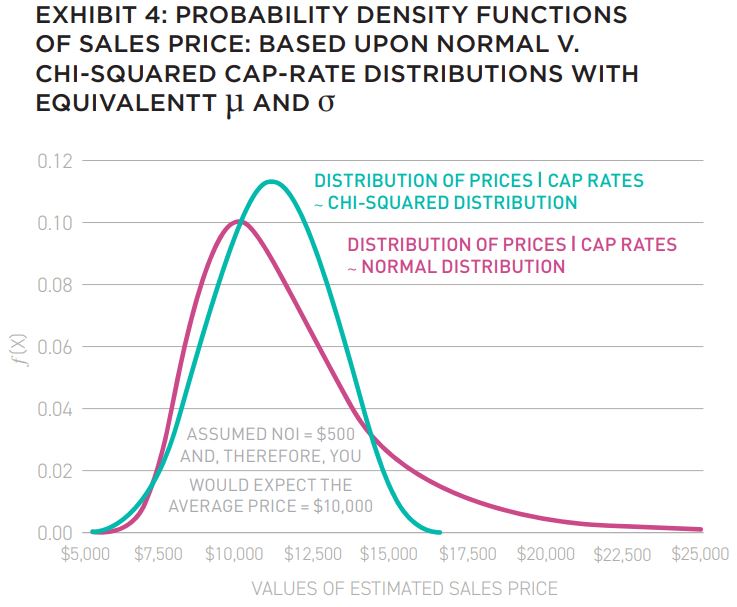
At first blush, it’s a bit surprising that the symmetrical distribution of cap rates (i.e., the normal distribution) produces the positively skewed distribution of prices (i.e., extremely high prices).7 Given today’s investment climate, the exceedingly high prices associated with the normal distribution seem unattainable.

Instead, it is the asymmetrical chi-squared (or χ2 ) distribution (i.e., with its fat right-tail) of cap rates that produces a near-symmetrical distribution of potential sale prices.

The interplay of price convexity and the assumed dispersion of cap rates also produces interesting first-two moments (µ and σ), under the two distributions, for estimated sales prices, as shown in Exhibit 5:

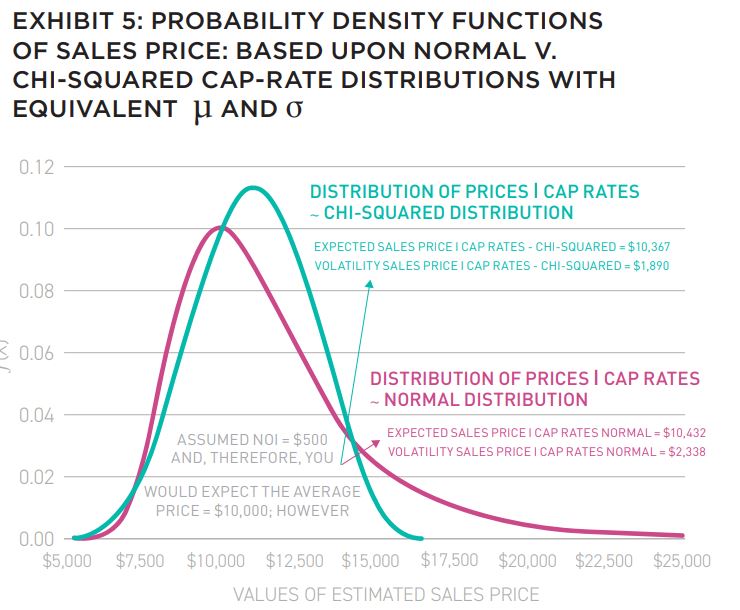
Consider the summary statistics for each distribution, starting with the expected values: the expected property price is approximately $10,432 under the normal distribution and $10,367 under the chi-squared distribution.

Note that the expected prices are higher than the estimated price ($10,000) assuming no uncertainty (or dispersion) in anticipated cap rates. The difference is due to the combination of price convexity and uncertainty. (This is another example of the adage associated with non-linear relationships: “The expectation of the average differs from the average expectation.”)

Additionally, the standard deviation of property prices is approximately $2,338 under the normal distribution, but only $1,890 under the chi-squared distribution; on a relative basis, the volatility of property prices is greater under the normal distribution (i.e., the coefficient of variation (σ/µ) ≈22.4% for the normal distribution and ≈18.2% for the χ2 distribution).

APPLICATIONS

Among many potential ramifications of the dynamics discussed here, consider four:

1. the lender’s estimate of its collateral value (the non-recourse lender effectively provides the borrower with a put option),
2. the developer’s estimate of land value is essentially a call option on the value of the future to-be- built project vis-à-vis the all-in costs of development,
3. the levered equity investor essentially owns a call option on the property’s value relative to the loan balance, and
4. the expected value of the general (or operating) partner’s carried interest is also a call option on the property’s future profitability.

The expected value of all such options depends on the volatility of the underlying asset. Investors (and lenders and modelers) beware!